日本語と英語で海外大学で学ぶ統計学入門レベルの基礎知識を簡単理解する

はじめに

この記事では、統計学入門レベルの専門用語を日本語・英語両方で確認し、その用語の内容は主に日本語で説明することで重要用語の意味を覚えよう、という趣旨で書いています。

筆者がUoPeopleのMATH1280のFinal Examのため、テスト2日前に入門レベルの統計学について１から復習した際のメモをもとに執筆しています。

数学的思考の基礎知識がない人間にとって、入門レベルであっても統計学の理解（特に計算）はとても難しいと感じました。

よって、計算の公式や、「計算を解いていくとこうだから、こうだ！」という証明や解説はひとまずさておき、重要単語の意味を理解し、説明文として書かれていることがわかるようになるレベルを目指しています。

もし、内容に不備を見つけてくださった場合は、ご遠慮なくコメントをお願いします。迅速に修正いたします。

おすすめの統計学入門書

本からしっかり基礎を押さえる時間的余裕のある方には以下の統計学入門レベルの本がおすすめです。

特に、「マンガでわかる統計学」がわかりやすいと評判です。

統計学入門の重要用語

Population(母集団)

何かを知りたいときの、対象全体のこと。

Sample（※後述）の全体のことではなく、Sampleにも含まれなかった部分を含む、その知りたいものの全体。

Sample(標本)

Population(母集団)から抽出した部分集合。

Mean(平均)

平均値のこと。Averageとも。

Median(中央値)

データが集計されると複数の値が確認される。値の順に並べた時、真ん中にくる値のこと。

Mode(最頻値)

データが集計された時、一番計測回数が多かった値のこと。

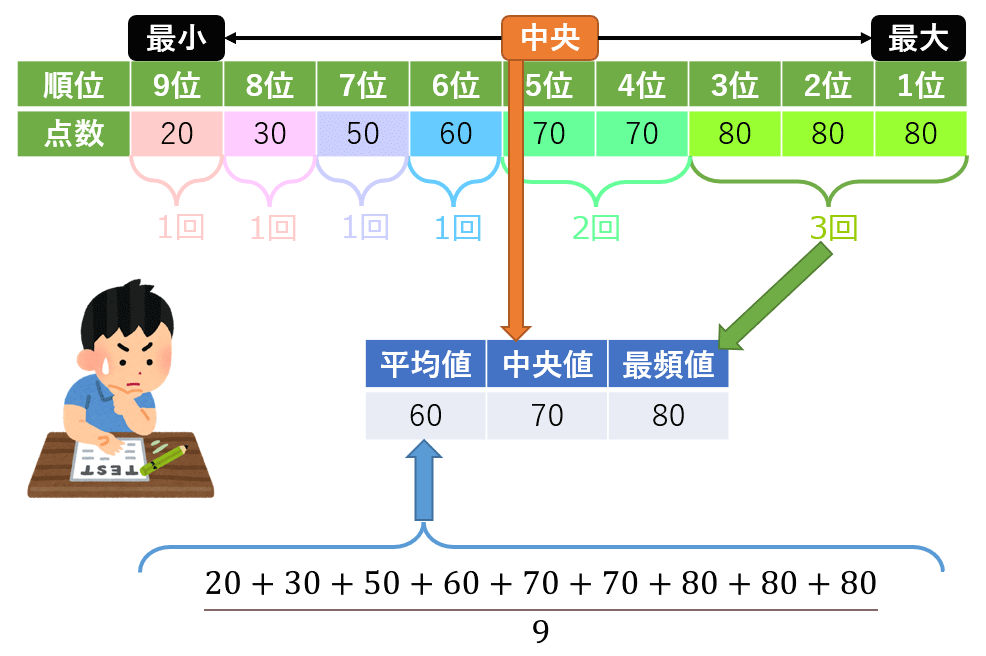
Mean/Median/Modeの違い

以下のITMediaさんのイラストが最高にわかりやすいです。

絵を見ていただけば解説は不要、ですね？

＠IT

平均値（Mean）／中央値（Median）／最頻値（Mode）とは？ 図1　代表値「平均値／中央値／最頻値」のイメージ

Quartiles(四分位数)

データを１列に並べて1/4ずつにした時に、その境界値となるデータ。データが小さい方から、1/4にしたところをQ1（データの25%）、2/4にしたところをQ2（データの50％、Median(=中央値)と一致）、3/4にしたところをQ3（データの75％）となり、Q4はデータの100％、何もデータを分割できないので統計で使用しない。Q1~Q3までが使用される。

小さい		平均		大きい
0%	25%	50%	75%	100%
Min	Q1	Q2(=Median)	Q3	Max

Interquartile Range (IQR)(四分位範囲)

四分位数を使用してデータのばらつきがわかる。Q1~Q3の範囲のこと。Q1~Q3の範囲から外れているデータは発生頻度が低い値と言える。

	←ーーーーーー	四分位範囲	ーーーーーー→
0%	25%	50%	75%	100%
Min	Q1	Q2(=Median)	Q3	Max

Quartile Deviation(四分位偏差)

Interquartile Range(IQR)を２等分にすると、Q1とQ3がどれくらい離れているかがわかる。

Parameter(パラメタ)

知りたいことのこと。統計を調査した結果では例えば平均値(Average/Mean)、割合(Percentage)、中央値(Median)、最大値(Max value)、最小値(Min value)などがそれに当たる。

補足

Parameterは不変だがStatistic(統計量)は取得したSampleに依存して値が変わるRandom Variable(確率変数)である。

Relative Frequency(相対頻度)

「クラス(階層、かな？)」がキーワード。実際のデータの値をクラスわけして、相対的にそのクラスが全体に対してどれくらいの頻度で発生するのか？を測る。

Cumulative Relative Frequency(累積相対頻度)

言葉通りCumulativeなRelative Frequency。各クラス分けが行われている場合、クラスは全ての発生しうる値をカバーしているべきで、クラスが全ての発生しうる値をしっかりカバーしている場合、各クラスの発生率はX%となりますね？その場合、各クラスの発生率を合計したら、100%(=1)になるはずです。

各クラスにおいて、そのクラスまでの値が発生する頻度（そのクラスの頻度だけではなく、そのクラス「まで（＝一番低いクラス~そのクラス）」の頻度）を表すのが、Cumulative Relative Frequency(累積相対頻度)です。

得点レンジ	クラス	相対頻度   （そのレンジの得点を取得した生徒の割合）	累積相対頻度   （一番下〜そのレンジを取得した生徒の割合）
90~100	A	10%	100%
60~89	B	60%	90%
0~59	C	30%	30%

Data Frame(データフレーム)

データを格納するオブジェクトのこと。「オブジェクト」と表示するとプログラマーっぽくなってしまうでしょうか…「データを格納するもの」「データを持ってくれる箱」みたいな解釈で良いと思います。多くの場合、「列」と「行」で構成される表形式で「２次元」の形でデータを持っていることが多いです。まぁ表の形でデータを保持できるものですね。

Variance(分散)

データの散らばり具合のこと。偏差（それぞれの数値と平均値の差）を二乗したものの平均を計算すると、その数値が出るらしいですが、用語解説だけでいうと「データの散らばり具合」です。

Sample Variance(サンプルの分散・標本の分散)

1つの標本のデータの分散具合。大きな母集団から１サンプル（標本）を取得し、データを見た場合のデータの分散具合。

Sampling Variance(サンプリングの分散)

Sample Varianceと言葉が似ていますが、内容は全然違います。

複数取得したサンプル達のばらつき具合のことです。取得したサンプルの平均値をそれぞれ計算して、１ヵ所に並べた時のばらつき具合。

Sampling Distribution(標本分布)

Sampling Varianceの分布のこと。複数のサンプルの平均値たちが、どのような形で表の中に分散するかを見る。

補足

Sample VarianceとSampling Varianceは、日本語での翻訳及び表現方法が一定に定まってはいないようです。

The Law Of Large Number(大数の法則)

試行回数が増えると、Samplie Average(サンプルの平均)が外れ値（平均から大きく外れた値）になる確率が小さくなる、というお話。

The Central Limit Theorem(中心極限定理)

この定理のおかげで、1サンプル（標本）あれば、Sampling Varianceを計算で知ることができる。標本分布には様々な形があるが、その形に依存しないのです。

Asymptotic Approach(漸進アプローチ)

1つの、バランスの取れたサンプルを使用してSampling Varianceを導き出します。

Bootstrapping Approach

1つのサンプルから、複数のサンプルを用意してテストを行なったようにシュミレーションをする導き方。

Random Variable(確率変数)

各事象は「確率」を持ち、その比率に応じて確率変数はランダムに値を取る。

Sample Space(標本空間)

試行の結果全体の集合のこと。

Probability(確率)

そのまま、「確率」のこと。0~1の間の値となる。

Expectation(期待値)

Random Variableの中央値。その事象を試行した場合、発生することが期待される値。

Binomial Random Variable(二項分布)

N回思考を行なった場合に、成功する回数の確率分布。「成功」と「失敗」２択のみの場合のお話。

「コインを投げたら表？裏？」というコイントスが例としてよく上がりますが、他にも成功か失敗で判断できる事象はたくさんありそうですね。

Poisson Random Variable(ポアソン分布)

ある期間内に平均N回発生することが、別のある期間にX回発生する確率の分布のこと。

Density(確率密度)

その値が、そのデータの中で相対的にどれくらい出やすいか。

Uniform Random Variable(一様分布)

連続型確率分布の1つ、と言われます。わかりやすくいくと、発生する確率が一定の値を取るものの分布。

Exponential Random Variable(指数分布)

「待ち時間の分布」と言われます。ある事象が何度も起きる時、次にその事象が発生するまでにどれくらいの時間がかかるか、というもの。

Normal Random Variable(正規分布)

データが平均値近くに集まる分布。

Standard Normal Distribution(標準正規分布)

平均が0、分散が1の正規分布のこと。

Percentile(パーセンタイル)※パーセンテージではない

データを大きい順に並べ、100で割った時、小さい方からどのくらいの位置にあるかを見る。

補足

パーセンテージ：50%＝そのデータのうちの半分のデータ

パーセンタイル：50 percentile=そのデータにおいて、50/100の位置にあるデータ

Normal Approximation of the Binomial(二項分布の正関近似=ラプラスの定理)

試行回数が多くなると、二項分布における確率が正規分布における確率に近くなる。

サンプルの取得とテストを繰り返すにつれて、正規分布の形に似てくる、というお話です。

Poisson Approximation of the Binomial(二項分布とポアソン分布)

二項分布の試行回数が増えても、その事象の発生回数が少ない場合はポアソン分布に似てくる、ということ。（反対に、発生する確率が高い時は正規分布に似てくる）

Random Sample(無作為抽出)

無作為にサンプルを抽出します。

Sampling Distribution(標本分布)

何回もサンプルを取得してテストした、それぞれのサンプルの分布。

References（参考サイト）

[simpleblogcard url=”https://best-biostatistics.com/toukei-kentei/ref_num.html”]

[simpleblogcard url=”https://bellcurve.jp/statistics/course/6984.html”]

[simpleblogcard url=”https://toukei.link/basicstatistics/population-sample-parameter-statistic/”]

[simpleblogcard url=”https://bellcurve.jp/statistics/course/6979.html”]

[simpleblogcard url=”https://ja.wikipedia.org/wiki/%E6%A8%99%E6%9C%AC%E7%A9%BA%E9%96%93″]

[simpleblogcard url=”https://kotobank.jp/word/%E7%A2%BA%E7%8E%87%E5%A4%89%E6%95%B0-43864″]

[simpleblogcard url=”https://ja.wikipedia.org/wiki/%E7%A2%BA%E7%8E%87%E5%A4%89%E6%95%B0″]

[simpleblogcard url=”https://datawokagaku.com/unbiased_variance/”]

[simpleblogcard url=”https://datawokagaku.com/unbiased_estimator/”]

[simpleblogcard url=”https://clover.fcg.world/2017/03/30/8379/”]

[simpleblogcard url=”https://data-viz-lab.com/iqr”]

[simpleblogcard url=”https://www.try-it.jp/chapters-6303/sections-6304/lessons-6329/”]

[simpleblogcard url=”https://atmarkit.itmedia.co.jp/ait/articles/2109/15/news033.html”]

[simpleblogcard url=”http://cse.naro.affrc.go.jp/takezawa/r-tips/r/39.html”]

[simpleblogcard url=”https://aiacademy.jp/media/?p=152″]

[simpleblogcard url=”https://www.greelane.com/ja/%e7%a7%91%e5%ad%a6%e6%8a%80%e8%a1%93%e6%95%b0%e5%ad%a6/%e6%95%b0%e5%ad%a6/frequencies-and-relative-frequencies-3126226/”]

[simpleblogcard url=”https://toukeigaku-jouhou.info/2018/03/31/percent-and-percentile/”]

[simpleblogcard url=”https://bellcurve.jp/statistics/course/7797.html”]

[simpleblogcard url=”https://bellcurve.jp/statistics/glossary/1207.html”]

[simpleblogcard url=”https://qiita.com/katsu1110/items/b0213c7ef6a8122abfc5#%E4%B8%80%E6%A7%98%E5%88%86%E5%B8%83-uniform-distribution”]

[simpleblogcard url=”https://bellcurve.jp/statistics/glossary/590.html”]

[simpleblogcard url=”https://ja.wikipedia.org/wiki/%E7%A2%BA%E7%8E%87%E5%AF%86%E5%BA%A6%E9%96%A2%E6%95%B0″]

[simpleblogcard url=”https://www.greelane.com/ja/%e7%a7%91%e5%ad%a6%e6%8a%80%e8%a1%93%e6%95%b0%e5%ad%a6/%e6%95%b0%e5%ad%a6/normal-approximation-to-the-binomial-distribution-3126589/”]

[simpleblogcard url=”https://manabitimes.jp/math/1107″]

[simpleblogcard url=”https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q13174792768″]

[simpleblogcard url=”https://physnotes.jp/2016-06-17/”]

[simpleblogcard url=”https://hsugaku.com/18-20″]

[simpleblogcard url=”https://navaclass.com/poisson/”]

[simpleblogcard url=”https://kotobank.jp/word/%E6%A8%99%E6%9C%AC%E5%88%86%E5%B8%83-121410″]

[simpleblogcard url=”https://ja.wikipedia.org/wiki/%E5%A4%A7%E6%95%B0%E3%81%AE%E6%B3%95%E5%89%87″]

[simpleblogcard url=”https://ja.wikipedia.org/wiki/%E4%B8%AD%E5%BF%83%E6%A5%B5%E9%99%90%E5%AE%9A%E7%90%86″]

[simpleblogcard url=”https://ai-trend.jp/basic-study/basic/central-limit-theorem/”]

[simpleblogcard url=”https://ebi-works.com/clt-proof/”]

[simpleblogcard url=”https://kotobank.jp/word/%E7%B5%B1%E8%A8%88%E7%9A%84%E6%8E%A8%E8%AB%96-103447″]

[simpleblogcard url=”https://bellcurve.jp/statistics/glossary/1421.html”]

[simpleblogcard url=”https://ja.wikipedia.org/wiki/%E7%82%B9%E6%8E%A8%E5%AE%9A”]

UoPeople関連の他記事はこちら！

Crescit eundo

UoPeople | Crescit eundo UoPeopleで学ぶアラサーエンジニアによる記録。文系卒、未経験からのエンジニア転職。コンピューターサイエンス専攻。残業だらけで時間の工面は大変ですが充実の毎日です！